
Ebben a fejezetben részben átismételjük a 9. évfolyamban tanultakat, részben kiegészítjük ismereteinket.
Két metsző egyenes négy darab szöget határoz meg. Közülük a szemköztiek csúcsszögek, a szomszédosok mellékszögek. Két metsző egyenes hajlásszögén a két mellékszög közül a nem nagyobbat értjü
k. Párhuzamos egyenesek hajlásszöge 0°. Két kitérő egyenes hajlásszögének nevezzük a tér egy tetszőleges pontján áthaladó, velük párhuzamos egyenesek hajlásszögét.Sík és egyenes, illetve két sík hajlásszögét még nem definiáltuk. Foglalkoztunk azonban az
egyenes és a sík merőlegességével: egy egyenes és egy sík akkor merőleges egymásra, ha az egyenes merőleges a sík minden egyenesére (definíció).Tétel (
A síkra merőleges egyenes tétele.): egy egyenes akkor és csakis akkor merőleges egy síkra, ha merőleges a sík két metsző egyenesére. A síkra merőleges egyenes tételét egyelőre nem bizonyítjuk.A továbbiakban tisztázzuk, hogy mit értünk sík és egyenes, illetve két sík hajlásszögén.
Az e egyenes messe az S
síkot, de ne legyen rá merőleges (51. ábra).
Vetítsük le merőlegesen az
S síkra az e egyenes minden pontját, így kapjuk az e’ egyenest. Az e egyenes és az S sík hajlásszöge definíció szerint egyenlő az e és e’ egyenesek hajlásszögével (az ábrán az a szög): ha egy egyenes metsz egy síkot, de nem merőleges rá, akkor a síkkal alkotott hajlásszögén a síkra eső merőleges vetületével bezárt szöget értjük.Két sík hajlásszögének értelmezéséhez tekintsük meg az 52. ábrát.
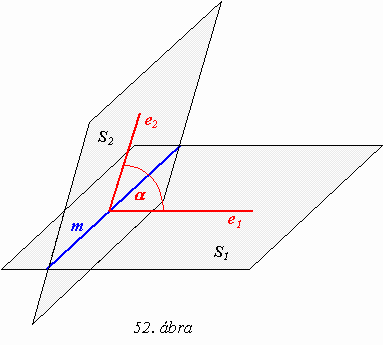
Az S1, S2
metsző síkok metszésvonala legyen m. A metszésvonal egy pontjában állítsunk m-re merőleges egyeneseket az egyes síkokban (e1 és e2). Definíció szerint az e1, e2 egyenesek hajlásszöge a két sík hajlásszöge: metsző síkok hajlásszögén a metszésvonal egy pontjából az egyes síkokban a metszésvonalra állított merőleges egyenesek hajlásszögét értjük.
Bizonyítás nélkül elfogadjuk, hogy tetszőleges
A, B pontokhoz tartozik egy nemnegatív valós szám, amely méri a két pont távolságát. (“Szemléletesen” az A és B pontok távolsága megmutatja, hogy az AB szakasz hossza hányszorosa az egységnyi hosszúnak választott szakasz hosszának.) Az A és B pontok távolságát d(A; B)-vel, vagy AB-vel (esetlegKét tetszőleges ponthalmaz távolságán az egymáshoz legközelebbi pontjaik távolságát értjük, ha ilyen pontok léteznek. A H és G ponthalmazok távolságát d(H; G)-vel jelöljük. (A P pont és az S sík távolsága: d(P; S).) A definíció néhány következménye:
Példa olyan ponthalmazokra, amelyeknek nincs távolsága: az AB és CD nyílt szakaszok legyenek egy egyenesen úgy, hogy ne legyen közös pontjuk (53. ábra).

Az AB és CD
szakaszoknak nincsenek egymáshoz legközelebb levő pontjai, mert a B illetve a C pontok nem tartoznak a szakaszokhoz.Kitérő egyenesek távolgágát az
54. ábra segítségével értelmezzük.
Az e és f
egyenesek kitérők. Az e egyenest eltoljuk önmagával párhuzamosan úgy, hogy messe az f egyenest (e’ egyenes), az f és e’ egyenesek határozzák meg az S2 síkot, az S1 sík tartalmazza az e egyenest és párhuzamos az S2 síkkal. Ezután vegyünk fel egy S3 síkot, amely merőleges az S1, S2 síkokra és tartalmazza az f egyenest. Mivel e és f kitérők (nincs közös síkjuk), az S3 síkot döfi az e egyenes. A döféspontban S1-re állított merőleges egyenes metszi e-t is és f-et is, valamint mindkettőre merőleges. Ezt az egyenest (t) az e és f kitérő egyenesek normáltranszverzálisának nevezzük. A normáltranszverzális segítségével definiáljuk a kitérő egyenesek távolságát: két kitérő egyenes távolsága a normáltranszverzális szakaszuk hossza. Belátható, hogy ez a definíció összhangban van a távolság általános fogalmával.
Térgeometriával, ezen belül a térbeli testek osztályozásával részletesen csak a 12. évfolyam anyagában foglalk
ozunk. Most csak néhány gyakran előforduló síklapokkal határolt test (poliéder) definícióját adjuk meg, illetve bizonyítás nélkül közlünk néhány térfogatszámítással kapcsolatos állítást. A legtöbb feladatban hasábokkal és gúlákkal találkozunk.A hasáb származtatása (55. ábra)

Egy sokszöget (az ábrán az A1B1C1D1E1F1 hatszög) toljunk el önmagával párhuzamosan (A2B2C2D2E2F2). Azt a térrészt nevezzük hasábnak, amit a sokszög az eltolás közben súrol. Az eredeti és az eltolt sokszög a hasáb alaplapjai
(néha alap- és fedőlap), az eredeti és az eltolt sokszög megfelelő pontjait összekötő szakaszok a hasáb alkotói, az alkotók összessége a hasáb palástja. Az alaplapok távolsága a hasáb magassága. Minden hasáb palástja paralelogrammákból áll (oldallapok).A hasáb térfogatát a V = Tm képlettel számítjuk, ahol V a térfogat, T az (egyik) alaplap területe, m a hasáb magassága.
Néhány speciális hasábra külön elnevezéseket használunk:
A gúla származtatása (56. ábra)

Egy sokszög (az ábrán az ABCDE ötszög) kerületének minden pontját kössük össze szakaszokkal egy a sokszög síkján
kívül eső ponttal (O). Az összekötő szakaszok és a sokszög határolta test a gúla. A sokszög a gúla alaplapja, az O pont a gúla csúcspontja, az összekötő szakaszok a gúla alkotói. Az alkotók összessége a gúla palástja, a palást háromszögekből áll (oldallapok). A gúla csúcspontjának az alapsíktól való távolsága a gúla magassága. A gúla térfogata ![]() , ahol V a térfogat, T az alaplap területe, m a gúla magassága.
, ahol V a térfogat, T az alaplap területe, m a gúla magassága.
Néhány speciális gúla:
A megismert geometriai transzformációkat, így a hasonlósági transzformációt is értelmezhetjük a térben is. Bebizonyítható, hogy a hasonló testek té
rfogatának aránya egyenlő a hasonlóság aránya abszolút értékének harmadik hatványával.